Who hasn't wondered at those magical curve balls that we see in sports such as tennis, soccer, baseball and most impressively in ping pong? Or been disappointed by a horrible slice in a game of golf? Of course, there is no magic, these are just examples of aerodynamics in action – the Magnus effect to be precise.

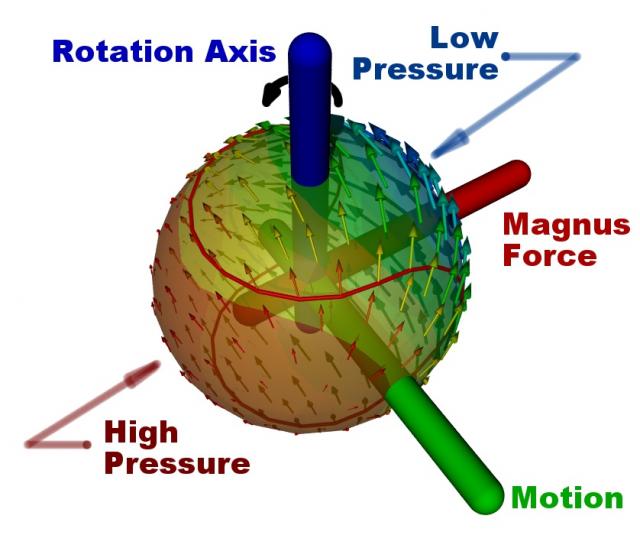Magnus Effect on a Spinning Ball Moving in Air

When sports players produce curve balls, be it through throwing, kicking or hitting a ball, they are exploiting the Magnus effect. Heinrich Magnus provided the first definitive description of this effect in 1853. However, there is some speculation that Isaac Newton also noted the same effect after, fittingly, watching a tennis match 180 years earlier.

The Magnus effect causes a spinning ball moving through air (or any other fluid such as water) to produce a force perpendicular to both its spin axis and its direction of travel. This force causes the ball to curve either left or right if the spin axis is vertical. If the spin axis is both horizontal and perpendicular to its direction of travel then the ball will either descend faster or slower than it would otherwise under the influence of gravity alone.

The classical explanation of the Magnus effect relies on Bernoulli's principle, which states that for an ideal fluid an increase in velocity is countered by a decrease in pressure and vice-versa. A good example of Bernoulli's principle is the Venturi effect as used in another sport driven (pardon the pun) by aerodynamics – motor racing. I digress; back to ball sports. As a spinning ball progresses through air, a thin vortex forms that attempts to rotate at the same speed as the ball. In the region where the vortex rotates toward the oncoming free-stream, the air close to the surface of the ball decelerates, causing the pressure there to increase. Conversely, where the vortex rotates away from the oncoming free-stream, the air accelerates, causing the pressure there to decrease. The difference in pressures on the surface of the ball causes it to change direction, just as pressure differences between the upper and lower surfaces of an airfoil produce lift.

While Bernoulli's principle provides an approximation of the Magnus effect, a more accurate model would include unsteady viscous effects driven by laminar and turbulent boundary layer separation, and the influence of the separated wake behind a ball. Still, the intuitive nature of Bernoulli's principle provides a good starting point for the seemingly magical curve ball phenomenon.