
Navier-Stokes Equations
Readers of Physics World, published by the Institute of Physics, voted Maxwell's equations and Euler's identity the greatest equations of all time. I guarantee if you posed the same question to mechanical engineers the Navier-Stokes equations would figure near the top, probably second to Newton's F = ma.
Computational Fluid Dynamics Available Now
Are you ready for a 30-day free trial of Caedium Professional?
Navier Stokes Equations
The Navier-Stokes equations assume a fluid to be a continuum, whereas in reality a fluid is a collection of discrete molecules. This continuum assumption holds up remarkably well and, when combined with linear and angular momentum conservation laws, results in the Navier-Stokes equations:
The Navier-Stokes equations mimic gas and liquid flow in all their turbulent complexity. It's a shame that there isn’t a single known analytic solution for them. However, if you happen upon such a solution or you can confirm there isn't a solution, be sure to claim the $1,000,000 prize on offer by the Clay Mathematics Institute as part of its Millennium Prize Problems.
CFD
Fortunately for aircraft designers and Formula 1 racecar aerodynamicists the discipline known as Computational Fluid Dynamics (CFD) solves simplified versions of the Navier-Stokes equations using numerical techniques on powerful computers. CFD applied to complex geometry and physics can take days or even weeks to produce results. For forced convection problems, such as the airflow over a wing or the water flow along a pipe, CFD can accurately mimic the real world, in terms of predicted fluid velocity and pressures.
 CFD Flow CalculationSymscape does not hold the copyright on this picture
CFD Flow CalculationSymscape does not hold the copyright on this picture
Numerical models of the Navier-Stokes equations are also the basis for weather forecasts. Wait, I hear you say, aren't forecasts notoriously inaccurate? Correct, but that is due to the chaotic nature of the underlying physics which the Navier-Stokes equations mimic. It's the uncertainty of the initial conditions in weather forecasting that leads to inaccuracy. Compounding the problem is the need to produce a timely forecast – today's forecast is useless if it arrives tomorrow.
Global Warming
The Navier-Stokes equations also play a leading role in global climate modeling and its prediction of Global Warming due to greenhouse gases such as carbon dioxide. Unlike weather forecast models, climate models are not constrained to make a prediction about tomorrow's weather. Liberated from immediate predictions, climate models can take more time to compute results and can be tuned to match eons of existing data.
History
With all the relatively recent activity in modeling the Navier-Stokes equations, instigated by the introduction of computers, you'd think they were a new discovery. You'd be wrong. The Navier-Stokes equations have been around since 1845, resulting from an intense effort over 18 years, when Navier, Cauchy, Poisson, St. Venant and Stokes introduced the idea of friction (viscosity) into the frictionless Bernoulli's equation derived by Euler in 1755. There the equations stood, a full and complete description of fluid flow, including the enigmatic turbulence, without any means of solution until the advent of computers.
Numerical Modeling
The first phase of numerical modeling for the Navier-Stokes equations requires a transformation to the Reynolds Averaged Navier-Stokes (RANS) equations. The RANS equations assume that time varying chaotic (turbulent) velocity fluctuations can be separated from the mean velocity. Once broken apart, the next step is to introduce a turbulence model to mimic the chaotic velocity fluctuations. With these two modifications the resources required to numerically solve the Navier-Stokes equations are greatly reduced to the extent that present day computers can perform meaningful calculations. However, turbulence models are still an open area for research. Turbulence models are typically tuned for particular applications such as problems with boundary layers, or shear layers, or mixing layers around jets. When the RANS equations are combined with the classical conservation laws (mass conservation and energy conservation) a powerful means to simulate real world fluid problems is possible. This form of modeling is the basis for nearly all engineering fluids simulations and has proven extremely effective. Everything from blood flow through the body to spacecraft re-entering the atmosphere have been simulated.
Worthy
Given the scope of the Navier-Stokes equations, I hope you agree they are worthy of a place in the greatest equations of all time, at least until the unified theory of everything is discovered, which will make all equations redundant.
Navier Stokes Lite
If you are interested in a lighter version of the Navier-Stokes equations that can run in a reasonable time on a laptop, then consider falling back to Bernoulli's equation. By assuming negligible viscosity and incompressible flow, a panel method (such as our Panel Flow add-on) can solve Bernoulli's equation to calculate the lift force around streamlined shapes such as an aircraft.
Recent blog posts
- CFD Simulates Distant Past
- Background on the Caedium v6.0 Release
- Long-Necked Dinosaurs Succumb To CFD
- CFD Provides Insight Into Mystery Fossils
- Wind Turbine Design According to Insects
- Runners Discover Drafting
- Wind Tunnel and CFD Reveal Best Cycling Tuck
- Active Aerodynamics on the Lamborghini Huracán Performante
- Fluidic Logic
- Stonehenge Vortex Revealed as April Fools' Day Distortion Field

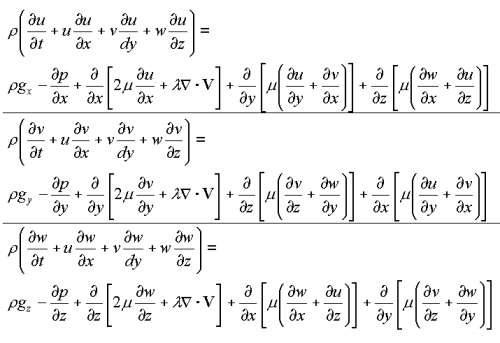
Comments
Another Vote for Euler's Identity
The journal Mathematical Intelligencer voted Euler's Identity (also known as Euler's Formula) the most beautiful equation of all time.
MILLENNIUM PRIZE PROBLEM (NAVIER– STOKES EQUATIONS)
MILLENNIUM PRIZE PROBLEM (NAVIER– STOKES EQUATIONS) IS SOLVABLE BY CLASSICAL METHODS
Kozachok A.A., Kiev, Ukraine
Formulated by Clay Mathematics Institute the sixth Millennium Problems about existence and smoothness of solutions of the Navier – Stokes equations periodically was discussed at numerous forums ( http://grani.ru/Society/Science/m.112524.html ). On recognition of some commentators the complete presentation of problem’s solution can demand about thousand pages for mathematical formulas ( http://lib.mexmat.ru/forum/viewtopic.php?t=4289 ). The author of Official Problem Description–Charles Fefferman has set the task about demonstration of existence and smoothness of the solution, instead of solution’s obtaining. However, the Navier-Stokes equations can be reduced correctly to more simple classical equations of mathematical physics . The problem of an existence proof of solutions of such equations is not so actual.
It is known, divu and divv are identical to infinitesimal magnitude and velocity of the relative modification of a volume element of the strained medium. Therefore divergency of acceleration divw, probably, there is a magnitude, identical to a acceleration of the relative modification of the same volume. In that case for incompressible liquid alongside with requirements divu=0, divv=0 it is necessary to accept divw=0.
The requirement divw=0 for incompressible liquid is formulated by analogy and proved. Operation div will convert the Navier – Stokes equations to the three-dimensional Laplace equation for pressure p=p(x,y,z,t) at some limitations of a mass force vector. The time enters into Laplace equation as parameter.
Laplacian of the Navier – Stokes equations (pressure p=p(x,y,z,t) – harmonic function) and a change of a variable (velocity on acceleration) allow to gain system of conventionally independent integro-differential equations with acceleration’s components w. In that case components of the acceleration for ideal incompressible liquid are harmonic functions too. The change of a variable allows to use boundary conditions of an adhesion of a fluid absolutely correctly. According to this requirement vectors of acceleration on firm immobile boundary line are equal to null.
Conversion of the Navier-Stokes equations to more simple equations has actually removed a problem of an existence proof and smooth finish of their solution on a background. Such demonstration in view of that one of required variables is a harmonic function, it is possible to not fulfil. It is possible to use known effects about properties of harmonic functions or representation of the common decision of the Laplace equation( http://continuum-paradoxes.narod.ru the link « Manual, p.1 », p. 58). More in detail on a site http://continuum-paradoxes.narod.ru the link “Russian pages”, “Sixth Millennium Problems (NAVIER-STOKES equations) is solvable by classical methods (in Russian)”.
Yours faithfully, Alexandr Kozachok
MILLENNIUM PRIZE PROBLEM (NAVIER– STOKES EQUATIONS) IS SOLVABLE
Read more here:
• Yet another solution proposed?
http://en.wikipedia.org/wiki/Talk:Navier%E2%80%93Stokes_existence_and_sm...