
Sports, Fluid Flow, and Spheres
Given how easy it is to define a sphere with a single value (radius) you'd think the fluid flow around a sphere would be simple too, right? However, as with many innocuous looking fluid problems, our intuition is wrong. The resulting flow characteristics, especially the drag variation with fluid velocity, are wild. Why does this matter? One word - sports.
 CFD Simulation of Flow Around a SphereReynolds number 10,000, large unsteady asymmetric recirculation
CFD Simulation of Flow Around a SphereReynolds number 10,000, large unsteady asymmetric recirculation
Sports
Golf, tennis, table tennis, baseball, cricket, basketball, soccer, any more? These sports can make grown adults euphoric and inconsolable, sometimes mere seconds apart, and all because of the flight of a round ball (sphere) through the air. The importance of making that sphere do and not do things cannot be underestimated - science to the rescue.
Drag
A governing factor on the trajectory of a sphere through the air is the drag force opposing its motion. And just to make sports more fun, the flow around a sphere is characterized by a massive variation of drag which is dependent on the Reynolds number. Or stated another way, if you keep the fluid properties (viscosity and density) and sphere diameter constant, the drag varies according to velocity.
 Experimental Drag Coefficient Variation with Reynolds Number
Experimental Drag Coefficient Variation with Reynolds Number
In many ball sports the Reynolds number lies close to 105. Notice that this Reynolds number falls close to the sudden drop off in drag? A coincidence? I think not! That is precisely where excitement, at least at the physics level, is interjected into ball sports. The sudden increase in drag for a decelerating ball makes the deceleration all the more pronounced giving rise to 'impossible' soccer free kicks.
Did you spot the loophole in the rules? You can also enter into the low drag club by strategically roughening the sphere. If your goal is for maximum speed (e.g., cricket, baseball) or maximum distance (e.g., golf), then you should roughen your ball. Of course tampering with the ball in cricket and baseball is against the other rules. However, golf positively embraces the rough with the sanctioning of dimples on golf balls.
 CFD Simulation of Flow Around a SphereReynolds number 100,000, steady small symmetric recirculation
CFD Simulation of Flow Around a SphereReynolds number 100,000, steady small symmetric recirculation
The dimples on a golf ball force the laminar boundary layer upstream of the separated turbulent wake region behind the ball to transition to turbulence. The turbulent boundary layer then entrains more energy from the surrounding flow, which reduces the size of the turbulent wake behind the ball and therefore reduces the overall drag of the ball.
Lift
Another way to affect ball trajectories is to add spin. A spinning sphere will experience a lift force by adding back spin relative to the direction of motion due to the Magnus Effect.
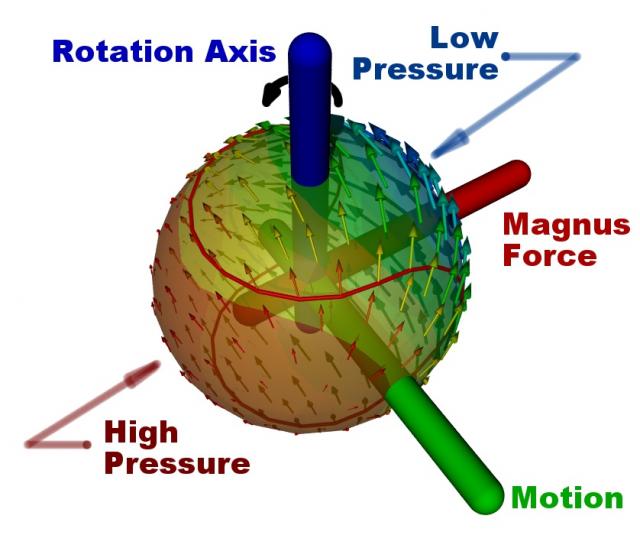 Magnus Effect on a Spinning Ball Moving in Air
Magnus Effect on a Spinning Ball Moving in Air
As a spinning ball progresses through air, a thin vortex forms that attempts to rotate at the same speed as the ball. In the region where the vortex rotates toward the oncoming free-stream, the air close to the surface of the ball decelerates, causing the pressure there to increase. Conversely, where the vortex rotates away from the oncoming free-stream, the air accelerates, causing the pressure there to decrease. The difference in pressures on the surface of the ball causes it to change direction, just as pressure differences between the upper and lower surfaces of an airfoil produce lift.
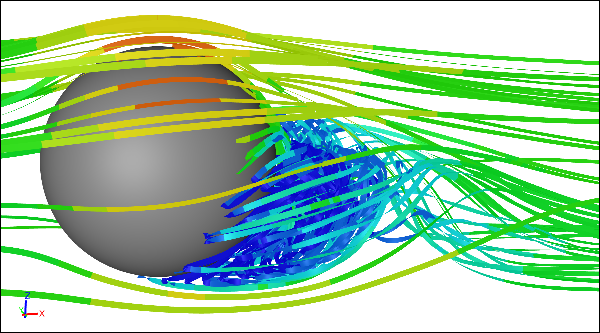 CFD Simulation of Flow Around a SphereRotating sphere, steady asymmetric recirculation
CFD Simulation of Flow Around a SphereRotating sphere, steady asymmetric recirculation
Any table tennis player will readily demonstrate that you don't just have to use spin for lift. You can apply top spin to make a ball dive downwards or apply side spin to make a ball curve sideways.
End Game
Just another example of a seemingly simple shape producing complex fluid behavior, but I'm glad otherwise how boring, from a physics perspective, would our favorite ball sports be?
Notes
- Experimental data best fit curve for a smooth sphere: Faith A. Morrison, "Data Correlation for Drag Coefficient for Sphere", Department of Chemical Engineering, Michigan Technological University, Houghton, MI.
- Simulations were created in Caedium Professional using the incompressible, steady-state RANS solver with the realizable k-epsilon turbulence model (fully turbulent).
- Idealized potential flow (no recirculation) tutorial "Fluid Flow Around a Sphere".
Recent blog posts
- CFD Simulates Distant Past
- Background on the Caedium v6.0 Release
- Long-Necked Dinosaurs Succumb To CFD
- CFD Provides Insight Into Mystery Fossils
- Wind Turbine Design According to Insects
- Runners Discover Drafting
- Wind Tunnel and CFD Reveal Best Cycling Tuck
- Active Aerodynamics on the Lamborghini Huracán Performante
- Fluidic Logic
- Stonehenge Vortex Revealed as April Fools' Day Distortion Field

Comments
Challenging CFD
I would like to point out that "standard" CFD (i.e. not DNS) has an extremely challenging time with such sport geometries. Mankind has optimized the shapes through trial and error. CFD drag predictions can be anywhere from 30% to 100% off. Depending on the shape, lift can be just as challenging. For example, I believe, it took DNS to solve the golf ball problem with 1+ billion cells. Or, LES may do well for a smooth sphere, but if it is roughened up the drag predictions are poor with respect to Reynolds number and I'm not aware of a turbulence model that works reliably well. In this case, CFD can easily equal Colorful Fluid Dynamics only.