
Symmetry for CFD to the Rescue
Symmetry is a simple but powerful concept that you can use to speed up your Computational Fluid Dynamics (CFD) simulations and reduce your memory requirements. Join me in an exploration of a simple symmetry case.
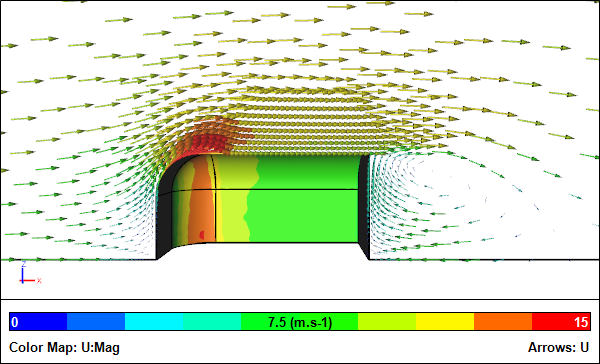 CFD Simulation of a Symmetric Quarter ModelVelocity vectors
CFD Simulation of a Symmetric Quarter ModelVelocity vectors
To benefit from symmetry you need to have geometric symmetry and flow symmetry. While geometric symmetry is usually easy to identify, flow symmetry is not obvious prior to running a simulation. For example, at certain Reynolds numbers the flow around a cylinder or sphere can be non-symmetric with unsteady vortex shedding.
Let's consider a simple cube with rounded edges and a blunt base that has half and quarter symmetry for comparisons. All the simulations use identical physics and solver settings in Caedium.
Full Model
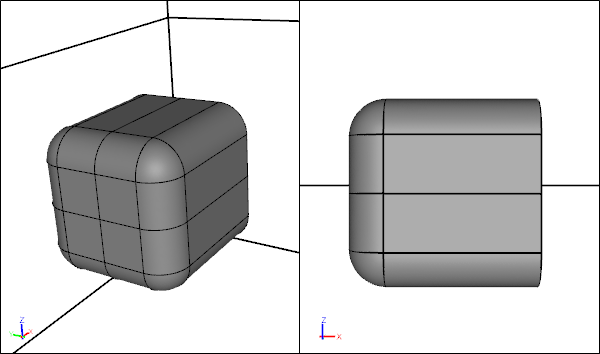 Full Model Geometry
Full Model Geometry
 Full Model CFD ResultsClipped velocity iso-surfaces
Full Model CFD ResultsClipped velocity iso-surfaces
Half Model
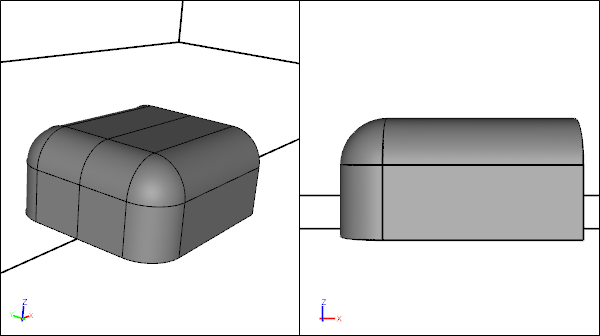 Half Model Geometry
Half Model Geometry
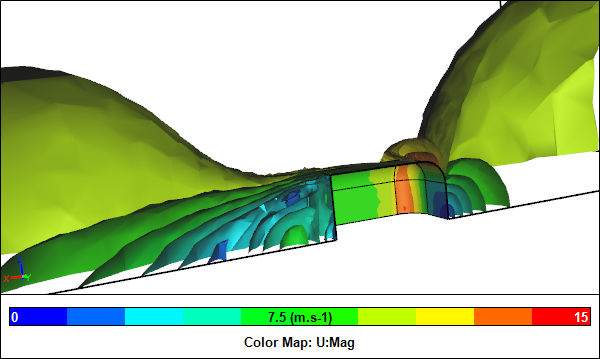 Half Model CFD ResultsClipped velocity iso-surfaces
Half Model CFD ResultsClipped velocity iso-surfaces
Quarter Model
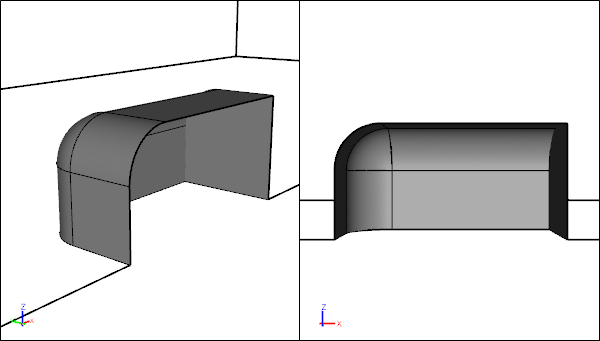 Quarter Model Geometry
Quarter Model Geometry
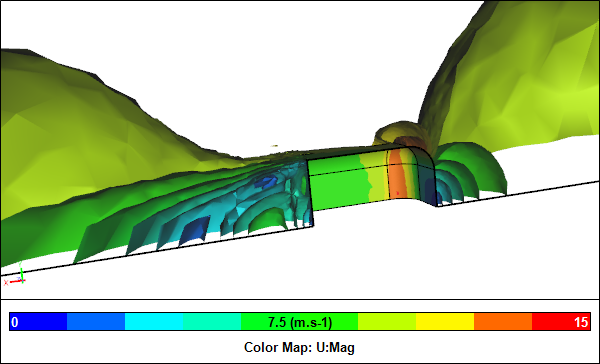 Quarter Model CFD ResultsVelocity iso-surfaces
Quarter Model CFD ResultsVelocity iso-surfaces
Comparison
| Full | Half | Quarter | |
| Cell No. | 322,249 | 161,761 | 81,866 |
| Cell No. % | 100 | 50 | 25 |
| Node No. | 59,628 | 30,869 | 16,100 |
| Node No. % | 100 | 52 | 27 |
| Drag (N) | 19.4 | 19.0 | 18.7 |
| Drag % | 100 | 98 | 96 |
| Clock Time (s) | 213 | 107 | 58 |
| Clock Time % | 100 | 50 | 27 |
Percentage values are relative to the full model without symmetry. The drag values for the half model where multiplied by two and the drag values for the quarter model were multiplied by four.
Conclusion
You can see the results for all 3 cases are similar. The quarter model simulation requires 75% fewer mesh elements compared to the full model and therefore requires 75% less memory. Also the quarter model runs 73% faster than the full model simulation for the same level of convergence.
Half symmetry is typically more common than quarter symmetry and produces a 50% saving in memory and 50% faster turnaround time compared to the full model simulation. Half symmetry is especially useful for external aerodynamic simulations of cars and airplanes.
Notes
Each model was created in Caedium Professional. The CFD simulations were performed using the incompressible, steady-state RANS solver on the dual mesh (i.e., a polyhedral mesh where the cell count is equal to the number of nodes in the original mesh), with the k-omega SST turbulence model.
Recent blog posts
- CFD Simulates Distant Past
- Background on the Caedium v6.0 Release
- Long-Necked Dinosaurs Succumb To CFD
- CFD Provides Insight Into Mystery Fossils
- Wind Turbine Design According to Insects
- Runners Discover Drafting
- Wind Tunnel and CFD Reveal Best Cycling Tuck
- Active Aerodynamics on the Lamborghini Huracán Performante
- Fluidic Logic
- Stonehenge Vortex Revealed as April Fools' Day Distortion Field
