
Potential Flow Around an Ellipsoid
Comparing a computation for the flow around an ellipsoid from our Panel Flow add-on with exact analytic potential theory is a good test (or verification) of our panel method implementation.
Theory
The potential (inviscid) flow around an ellipsoid reduces to the analytic equation:
u / Uinf = ( Umax / Uinf ) . sqrt[ ( 1 - x2 ) / ( 1 - x2 . a2 ) ]
a2 = 1 - r2
Umax / Uinf = 2 / (2 - b)
b = 2 [ ( 1 - a2 ) / a3 ] . ( atanh(a) - a)
where:
u is the surface velocity magnitude
Uinf is the free stream velocity magnitude assumed parallel to x-direction
x is the distance from center assuming overall length is 2
r is the radius at x = 0 (in this case r = 0.2)
Results
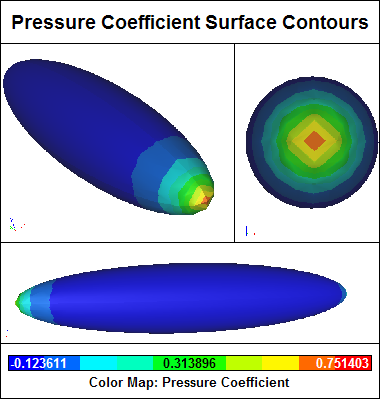
Pressure coefficient surface contours.
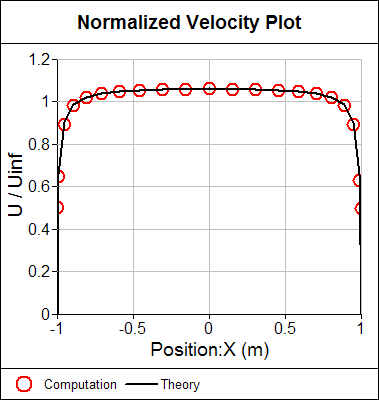
Normalized velocity comparison between potential flow theory for an ellipsoid and computation.
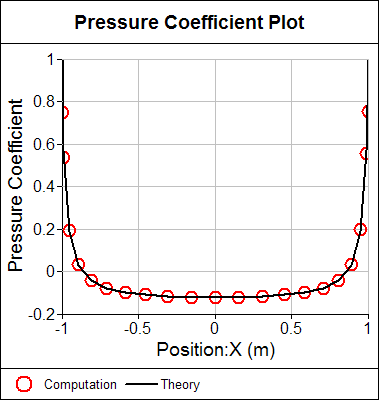
Pressure coefficient comparison between potential flow theory for an ellipsoid and computation.
Notice the excellent agreement between the computation and the theory.
Try For Yourself
The sym project file for this study can be viewed in Caedium or you can investigate this case yourself using our Panel Flow add-on.
The most convenient way to view and edit this case is to use our Professional add-on that combines all the add-ons used during this example.
- Login to post comments

