Many see the future of automobiles to be electric, so it's only natural to assume that the same may apply to motor racing. Luke Horsfall is one who believes electric race cars have a bright future, having set up Horsfall Racing (along with Laura Horsfall) to build electric race cars and race them in the F24+ electric race car class in the UK. The restrictions of this particular formula keep budgets and speeds relatively low (at least by Formula 1 standards). Making best use of the limited power in F24+ is crucial, and that places the emphasis on low-drag, aerodynamic race cars. I bet you can guess where this is heading - this is territory ripe for Caedium's Computational Fluid Dynamics (CFD) capabilities.

Super Swoosh:Horsfall Racing's 2009 Electric Race Car

Background

Horsfall Racing's chief designer Luke Horsfall has produced 7 generations of electric race cars, dating back to his school days. For his most recent, 8th generation design he has turned to CFD as a cost-effective means to help optimize the aerodynamics of his car. Unlike F1 there's little use in sacrificing drag for downforce in such relatively low-powered cars, so the aerodynamic design focuses on minimizing drag, which favors a sleek-streamlined exterior. Luke recently enlisted Symscape to help with the CFD analysis of his latest design for the upcoming 2010 season.

Geometry

Luke's latest race car design was created in a CAD system, so a STEP geometry file was used to transfer the geometry into Caedium Professional. Using the various geometry creation and fixing tools in Caedium the original geometry was modified in order to represent the volume of air surrounding the car. By assuming a symmetric car and flow field, only half of the flow volume is needed for the CFD simulation. Symmetry allows the simulation to run twice as quickly and only use half the memory that would otherwise be necessary.

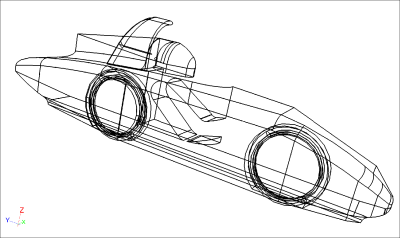Original Geometry

Physics

The CFD simulation setup included:

• Free-stream air speed and moving-ground speed = 15 m/s (54 km/h or 34 mph)
• Wheel rotation speed = 666 rpm
• k-omega SST turbulence model

The race car, its wheels, and the ground plane were specified as walls (impregnable by air). Additionally the wheels were assigned a rotational speed and the ground plane was configured with a linear speed matching the free-stream air speed. The sides and ceiling of the flow volume were specified as symmetry planes to simulate the other half of the flow volume and mimic free air. The upstream face was specified as an inlet and the downstream face was specified as an outlet.

Results

Front View of Velocity

Rear View of Velocity

Front View of Pressure

Rear View of Pressure

Front View of Streamlines

Rear View of Streamlines

The drag coefficient (C_D) was 0.19.

Conclusion

Clearly Luke's experience in designing low-drag race cars is evident in this latest design when you compare its C_D = 0.19 to that of a typical passenger car, such as a Honda Civic with C_D = 0.31.