Are you wondering how a polyhedral (dual) mesh compares to the equivalent tetrahedral and hexahedral meshes? Then you're in the right place. This study compares the volume element count, convergence, accuracy, and runtimes of the three different types of meshes for a simple duct.

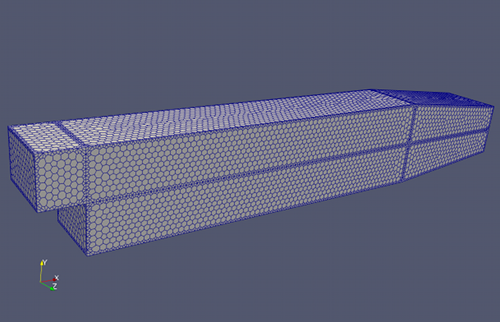Polygon Surface Mesh: Backward facing step in a duct

This study focuses on a 3D backward facing step within a duct. The duct geometry was decomposed into 6-faced blocks so it could support a hexahedral mesh as well as the more general tetrahedral and polyhedral meshes.

Meshes

Slices through the meshes revealing volume elements are shown below.

Hexahedral Volume Elements

Polyhedral Volume Elements

Tetrahedral Volume Elements

The polyhedral mesh is derived directly from the tetrahedral mesh by forming polygons around each node in the tetrahedral mesh.

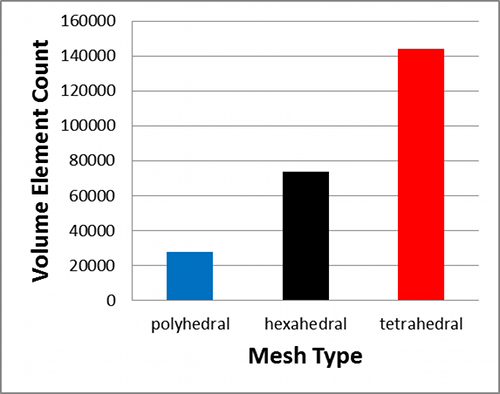Volume Element Counts

Convergence

The pressure residual for each mesh type is show below.

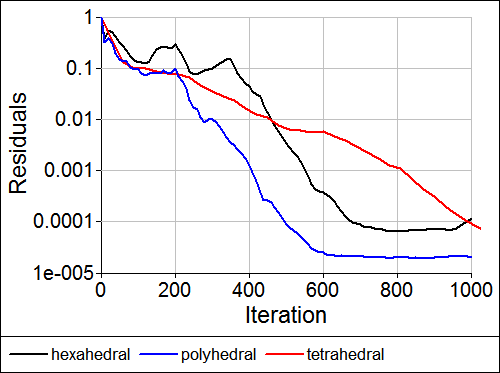Pressure Residuals Monitor

The solution on the polyhedral mesh produced the lowest absolute residual value.

The number of iterations for each mesh type to reach the same level of convergence (1x10^-4) for the pressure residual are shown below.

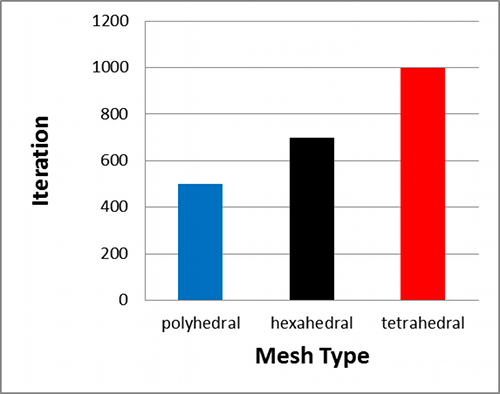Pressure Residual Convergence

Accuracy (Pressure Drop)

The pressure drop for each mesh type is shown below.

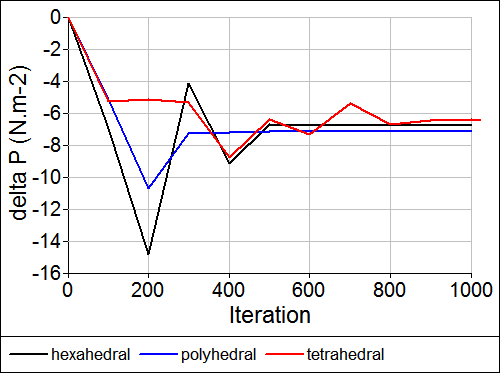Pressure Drop Monitor

While there are minor differences in the converged pressure drop the simulations are in broad agreement on the overall value.

The number of iterations for each mesh type to reach a steady state value for the pressure drop are shown below.

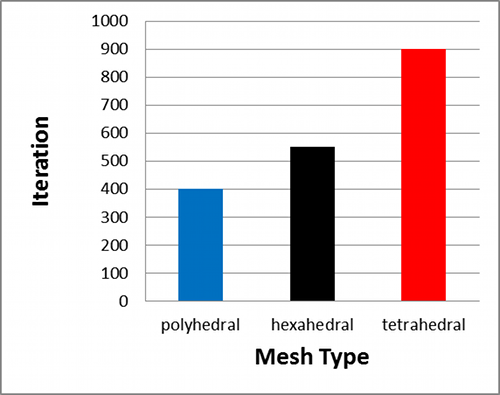Pressure Drop Convergence

Runtime

Assuming our goal is to reach the steady state pressure drop for each simulation, then the runtimes (scaled against the slowest simulation) are shown below.

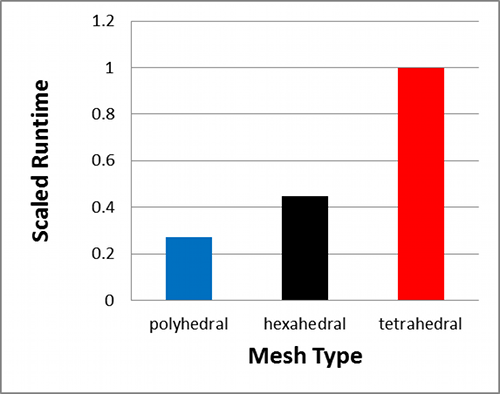Runtimes

Conclusions

Cleary this study shows that polyhedral cells hold great promise in producing equivalent accuracy results compared to other mesh types with the added benefits of:

• Faster converge with fewer iterations
• Robust convergence to lower residual values
• Faster solution runtimes