
A Case for Renaming the Navier-Stokes Equations
You probably know that the Navier-Stokes (NS) equations are named after Claude-Louis Navier and George Gabriel Stokes. Navier come up with the first original derivation based on discrete molecular interactions (discrete approach) and Stokes originated the assumption of a continuum directly using viscosity that is the widely referenced approach still taught today. However, between these two approaches there were other derivations, a continuum of sorts, attributed to other luminaries of 19th Century science.
 Navier (left) and StokesRoom for more?
Navier (left) and StokesRoom for more?
Navier started the flow in the derivation of the NS equations in 1822, but before Stokes concluded with his definitive derivation in 1845 there were:
- Augustin-Louis Cauchy in 1828
- Simeon Denis Poisson in 1829
- Adhemar Jean Claude Barre de Saint-Venant in 1843
As a prequel to the NS equations, Leonhard Euler in 1757 derived his inviscid (viscosity free) flow Euler equations, which are a subset of the full NS equations. Navier through to Stokes all derived their respective equations using the Euler equations as a starting point.
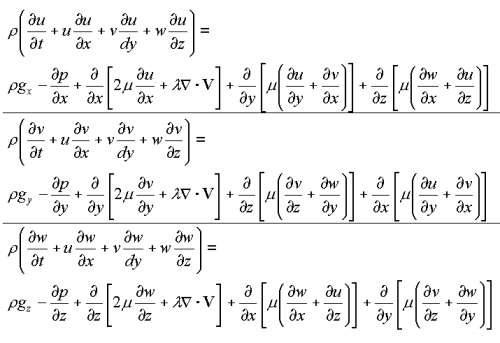 Navier-Stokes Equations
Navier-Stokes Equations
While there is no doubt that the NS equations are complex and have caused many an undergraduate studying fluid dynamics to have nightmares, at least the name historians agreed upon was relatively simple. If full credit was to be reflected in the naming of the equations then we should surely consider (in chronological order of course!):
The Euler-Navier-Cauchy-Poisson-Saint-Venant-Stokes equations or ENCPSS (pronounced encompass) for short.
Such a name would be a much more worthy way to strike fear into anyone who dares to go near them - matching the complexity of the equations themselves.
Luckily for most engineers interested in fluid dynamics they can instead stand on the shoulders of these and other giants (e.g., Osborne Reynolds) to realize the power of solving the NS equations in simplified form using Computational Fluid Dynamics rather than worry about their derivation.
Recent blog posts
- CFD Simulates Distant Past
- Background on the Caedium v6.0 Release
- Long-Necked Dinosaurs Succumb To CFD
- CFD Provides Insight Into Mystery Fossils
- Wind Turbine Design According to Insects
- Runners Discover Drafting
- Wind Tunnel and CFD Reveal Best Cycling Tuck
- Active Aerodynamics on the Lamborghini Huracán Performante
- Fluidic Logic
- Stonehenge Vortex Revealed as April Fools' Day Distortion Field
