I don’t think anyone would argue with the fact that paper airplanes are simple (and fun!), but what is the simplest paper airplane that can still fly? I give you a single rectangular piece of paper without any folds that will gently spin around its longest horizontal axis if released with a long edge parallel to the ground. Next, what is the simplest Computational Fluid Dynamics (CFD) method that can capture the essence of the spinning paper? I give you the Moving Reference Frame (MRF, also known as the frozen rotor method) option for CFD. Combine the two and you arrive at an interesting simulation of a simple phenomenon.

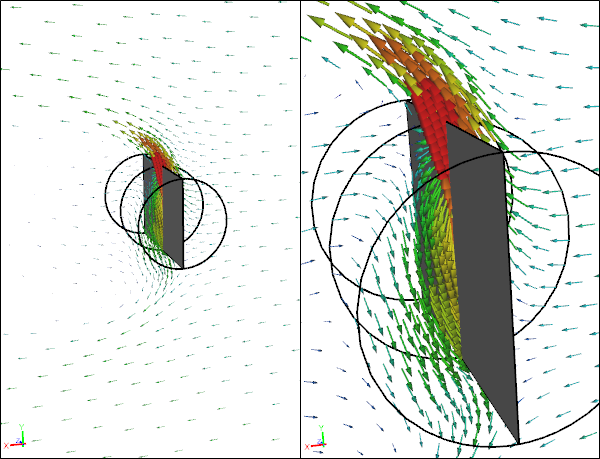CFD Simulation of a Rotating Paper SheetVelocity vectors at 90 degrees

Recall that a MRF is an approximation to a spinning motion, so the results from such an approach will not be perfect, but they are nevertheless useful and insightful.

CFD Model

The CFD model for this simple paper airplane consisted of a zero-thickness, double sided face to represent the paper sheet, embedded within a MRF cylinder, which was embedded in a larger cylinder representing the outer extent of the flow domain. Due to symmetry, and to save resources, I only modeled half of the flow domain.

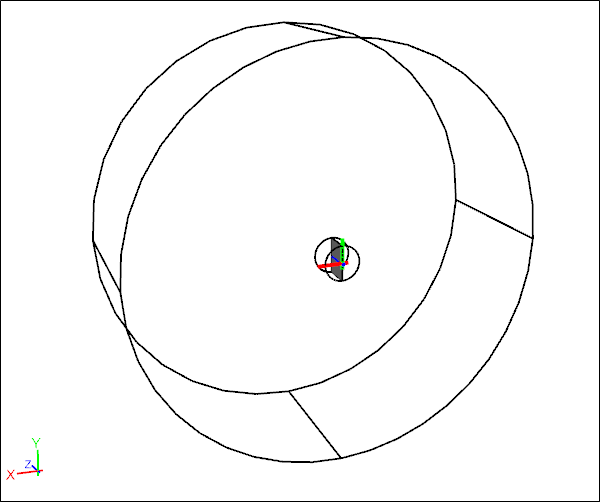CFD MRF Symmetry 3D Model of a Rotating Paper Sheet

Results

To obtain flow results at various angles of the paper sheet I used automation via a Python script to rotate the geometry and run a series of CFD simulations. The lift and drag values are collated in the plots below.

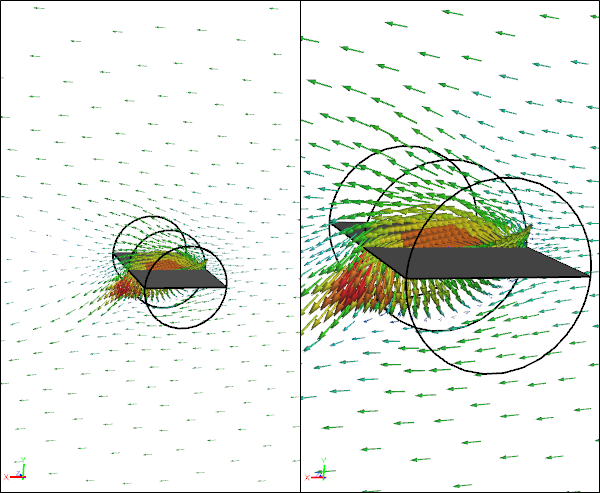Velocity Vectors for Rotating Paper Sheet at 0 Degrees

Velocity Vectors for Rotating Paper Sheet at 90 Degrees

Pressure Iso-Surfaces for Rotating Paper Sheet at 0 Degrees

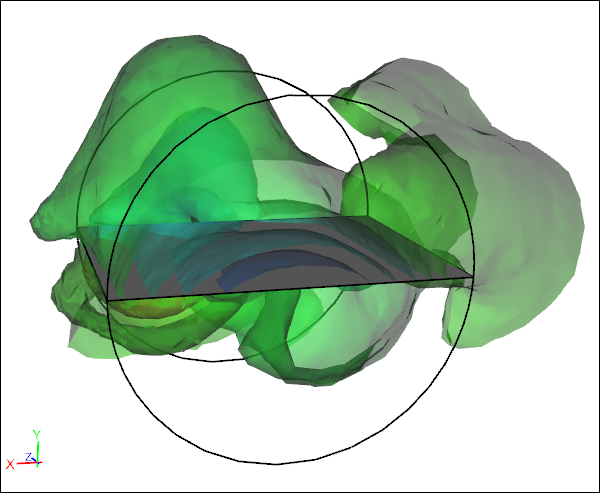
Pressure Iso-Surfaces for Rotating Paper Sheet at 90 Degrees

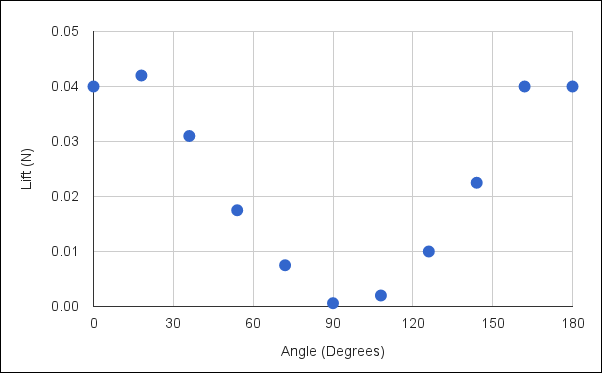Lift for a Rotating Paper Sheet

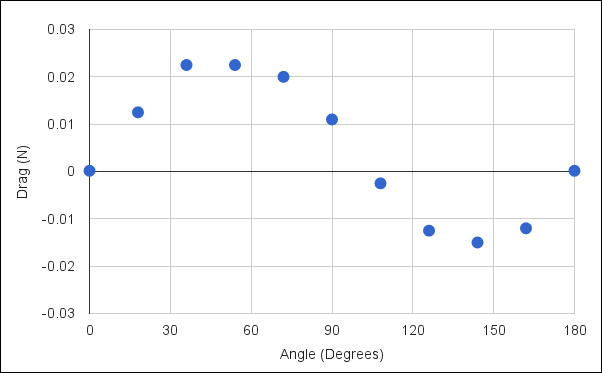Drag for a Rotating Paper Sheet

Conclusion

The lift and drag show a relatively smooth variation through the range of angles simulated. The lift peaks close to the horizontal position (i.e., 0 and 180 degrees) and approaches zero around a 90 degree inclination to the horizontal - resembling a 'U' shape. Interestingly, the drag resembles a sine wave and has negative values (thrust) between 100 - 180 degrees.

Notes

The CFD simulation was performed in Caedium Professional using the MRF option for the incompressible, steady-state RANS solver, and the k-omega SST turbulence model.