Comparing a computation for the flow around a sphere from our Panel Flow add-on with exact analytic potential theory is a good test (or verification) of our panel method implementation.

Theory

The potential (inviscid) flow around a sphere is equivalent to the superposition of a 3D doublet and a free stream, which reduces to the simple analytic equation:

C_p = 1 - 9/4 cos²(theta)

where:
C_p is the Pressure Coefficent
theta is the angle measured perpendicular to the flow direction

Results

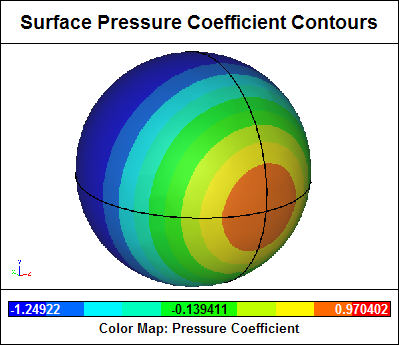
Surface Pressure Coefficient Contours.

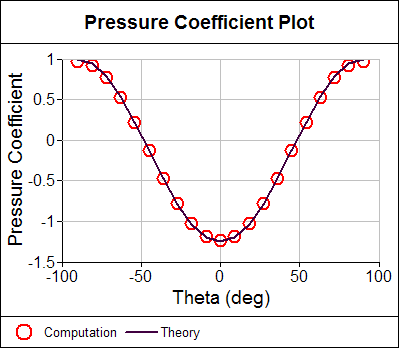
Pressure Coefficient comparison between potential flow theory for a sphere and computation.

Notice the excellent agreement between the computation and the theory.

Try For Yourself

The sym project file for this study can be viewed in Caedium or you can investigate this case yourself using our Panel Flow add-on.

The most convenient way to view and edit this case is to use our Professional add-on that combines all the add-ons used during this example.